ガウス分布の理解
Overview
- ガウス分布、または正規分布は、その象徴的なベル型曲線により特徴づけられます。
- これらの分布は、統計学、心理学、機械学習など、さまざまな分野で必ずしも不可欠であり、データ分析の基盤を形成します。
- その特性を深く理解することで、我々は多様な実世界の現象を効果的にモデル化し、予測する力を高めることが可能になります。
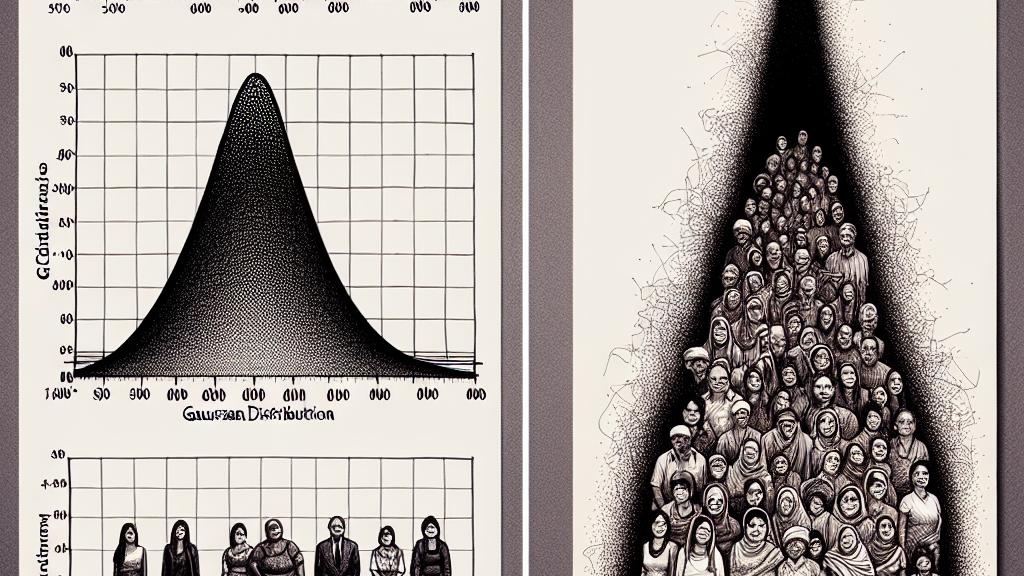
ガウス分布とは?
ガウス分布は、統計学の中心的な概念であり、その特徴は滑らかで対称的なベル型の形です。この分布は、多くの実世界の現象を理解するための強力なツールとなります。例えば、仮に1万人の成人女性の身長データを収集したとしましょう。そのデータをプロットすると、ほとんどの身長が平均の周りに集まり、高いピークが形成されるのが見えます。しかし、この現象だけが全てを物語るわけではありません。対照的に、富の分布を考えると、貧富の差が大きく、極端に富んでいる人や貧しい人が存在します。このように、ガウス分布は身長のような限られた変動を持つ現象を見事に描写しますが、富のような変動が大きい現象には適しません。このことは、ガウス分布がどのように特定のデータに対して正確な表現を提供するかを示しています。
実際の応用における重要性
ガウス分布を理解することは、学問的な成果だけでなく、実際の応用にも大きな影響を与えます。例えば、一般人口のIQスコアを考えた場合、これらのスコアをグラフにすると、美しいベルカーブが得られます。その平均は100で、非常に高いスコアや低いスコアを持つ人はほとんどいません。このようなデータを用いることで、教育者や政策立案者は知能分布をより明確に把握することができます。また、中心極限定理という理論も重要です。この理論によると、サンプルサイズが十分であれば、どんな元の分布でも平均値は正規分布に近づくと言われています。ここでの重要なポイントは、さまざまな現象を理解する手助けをするということです。たとえば、植物の高さや国ごとのテストスコアを分析する際、この理論は信頼できる方向性を提供してくれます。したがって、我々は多様なデータに基づいた結論を導き出すことができるのです。
機械学習とデータ分析における応用
急速に進化する機械学習の分野では、ガウス分布の役割は欠かせません。なぜなら、複雑なモデルを構築するための基盤であり、データにガウスノイズを加えることでリアルな不確実性を模倣できるからです。具体的に言えば、映画の推薦システムを開発する際、複数のガウス分布を使用することで、異なる文化や年齢層における視聴者の好みを捉えることができます。この結果、よりパーソナライズされた推薦が可能になります。ガウス分布を習得することにより、データサイエンティストは複雑なデータセットに対する深い理解を得られ、多彩な分析手法を駆使することができます。このスキルは予測精度を高め、アナリストが情報に基づいた戦略的な意思決定を行う手助けになります。したがって、ガウス分布の理解はデータ分析の複雑さを解明するための鍵であると言えるでしょう。

Loading...